CODEFES 2017-C 3 Steps

この記事はCODEFES 2017のC問題の解説の補足です。

1. どうして奇数長の長さだと繋げられるのか
2. 2部グラフじゃない場合、どうして完全グラフにすることができるのか

をより詳しくみていきます。

1. どうして奇数長の長さだと繋げられるのか

解説の通り、頂点Sと頂点Tにk個の辺があるケースを考えます。

下図の通り、3つの辺が1つの辺になるので、頂点Tに2つ少ない辺で到達できます。

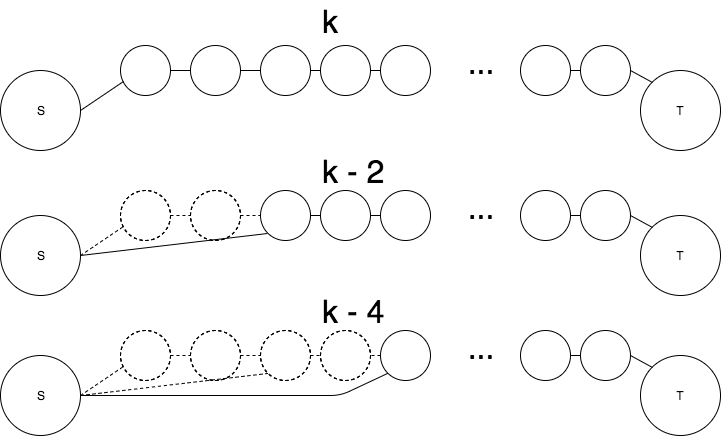
頂点Sと頂点Vは3つの辺で到達できるとき繋げられるので

k - 2n = 3 (nが整数でn >= 0)

が成り立つ時、つなげることができます。つまり、辺の数が奇数のときです。

2. 2部グラフじゃない場合、どうして完全グラフにすることができるのか

完全グラフとは、ある頂点から自身を除く全ての頂点へ辺があるグラフのことです。2部グラフじゃない場合、完全グラフにすることができると説明されています。これを、下のグラフで考えてみます。

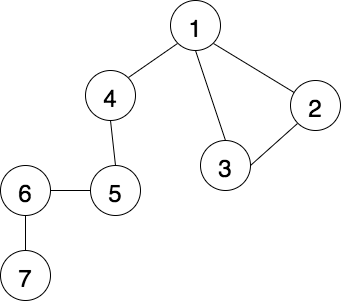
頂点を結ぶ辺が偶数の場合、頂点Sから頂点Tへ

1. ループを含む頂点を経由する (例: 4 -> 2)
2. ループを含む頂点を経由しない
   1. ループを含む頂点まで偶数個の辺でいける (例: 7 -> 5)
   2. ループを含む頂点まで奇数個の辺で行ける (例: 6 -> 4)

1の場合、途中でループを経由することで奇数を偶数に足すことができるので、経由する辺の数が奇数になります。

2.1の場合、頂点Sから頂点T(偶数)、頂点Tからループを含む頂点(偶数)、ループ(奇数)、ループを含む頂点から頂点T(偶数)となるので、すべて足すと奇数になります。

2.2の場合、頂点Sから頂点T(偶数)、頂点Tからループを含む頂点(奇数)、ループ(奇数)、ループを含む頂点から頂点T(奇数)となるので、すべて足すと奇数になります。

よって、2部グラフじゃない場合、すべての点へ奇数個の辺を経由していけるので、完全グラフになります。